Введение
Интересной разновидностью цифровых фильтров являются так называемые минимально-фазовые цифровые фильтры, которые широко применяются во многих приложениях цифровой обработки сигналов. Как известно, в минимально-фазовом фильтре все нули коэффициента передачи не выходят за пределы единичной окружности в z-плоскости, что, как правило, определяет меньший порядок фильтра и меньшее время обработки сигнала в сравнении с цифровыми линейно-фазовыми фильтрами. Для многих практических приложений это может иметь существенное значение. Условие минимальной фазы может быть реализовано как в цифровых фильтрах с бесконечной импульсной характеристикой (БИХ-фильтрах), так и в фильтрах с конечной импульсной характеристикой (КИХ-фильтрах), однако рекурсивные фильтры, являясь дискретными линейными системами с обратной связью, обладают значительно большими селективными возможностями в сравнении с КИХ-фильтрами и позволяют реализовать требуемые характеристики значительно меньшей разрядностью представления данных и меньшим порядком фильтра.
Как известно, классическая методология проектирования БИХ-фильтров реального времени, в том числе и минимально-фазовых, содержит два основных этапа: аппроксимации и практической реализации фильтра. На этапе аппроксимации формируется аналитическое представление заданной характеристики фильтра-прототипа
KT(ω) тем или иным аппроксимирующим полиномом, на базе которого в дальнейшем формируется передаточная функция проектируемого цифрового фильтра. Так, аппроксимация ФНЧ по Баттерворту (рис. 1а) определяется так:
Bn(ω) = 1 / (1+ω
2n).
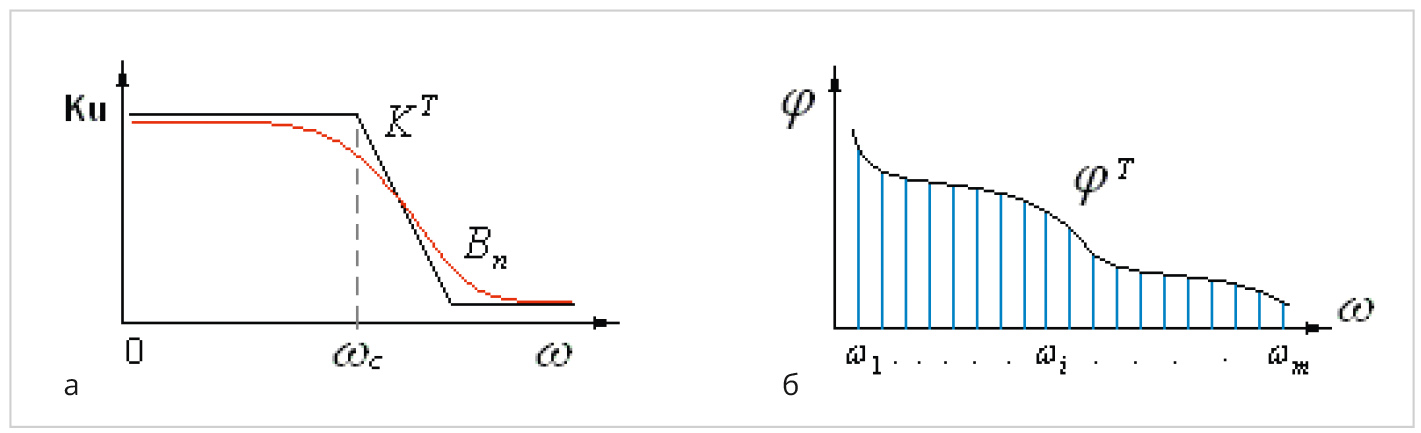
Таким образом, этапу аппроксимации свойственна систематическая ошибка, которую условно можно записать так:
δ
a = max
ω |
KT(ω) – B
n(ω)|.
Ошибка аппроксимации весьма ограничивает возможность реализации характеристик сложной формы приемлемым порядком аппроксимирующих полиномов. Поэтому аналитическое проектирование БИХ-фильтров по аналоговому прототипу ограничивается, как известно, только набором типовых форм требуемых характеристик (ФНЧ, ФВЧ, ППФ, ПЗФ), которые могут быть аппроксимированы с минимальной ошибкой.
Основными задачами этапа практической реализации фильтра как дискретной системы реального времени является, прежде всего, выбор арифметики цифровых вычислений и приемлемой длины слова коэффициентов фильтра для их реализации заданным числом двоичных разрядов. Наиболее часто для представления переменных в алгоритмах цифровой фильтрации используется вычисления в формате с фиксированной точкой M.N при M = 0 (где M – целая часть, N – дробная часть числа). В двоичном представлении фиксированная точка находится справа от самого старшего бита, который является обычно и битом знака. То есть все коэффициенты цифрового фильтра являются дробными вещественными числами, принадлежащими диапазону от –1 до 1–2–(Wk–1), где Wk – число битов, используемых для двоичного представления числа (включая знак). Однако заданным числом двоичных разрядов можно реализовать только дискретный ряд определённых значений коэффициентов на заданном единичном интервале. Так, 4-битовое представление в формате с фиксированной точкой (ФТ) определяет следующий ряд дискретных значений коэффициентов: Wk: {–1; –0,875; –0,75; –0,625; –0,5; –0,375; –0,25; –0,125; 0; 0,125; 0,25; 0,375; 0,5; 0,625; 0,75; 0,875}. Для 5-битового представления добавляются промежуточные значения и так далее.
Однако аналитический расчёт коэффициентов проектируемого БИХ-фильтра, например, билинейным преобразованием аналогового прототипа в пакете MATLAB, осуществляется только в непрерывном вещественном пространстве, то есть коэффициенты фильтра определяются с неограниченной точностью на единичном интервале их определения. Поэтому на стадии реализации проектируемого фильтра необходима процедура квантования вещественных его коэффициентов, которая в формате с ФТ осуществляется следующим образом: целочисленный код (квант) Сint вещественного неквантованного коэффициента |C| < 1,0 в варианте округления до ближайшего целого (round) равен целой части выражения в скобках:
Cint = int (C•2
Wk–1 + 0,5). (1)
Тогда вещественный квант
Сfloat данного коэффициента определяется так:
Сfloat = Cint / 2
Wk–1 , (2)
а ошибка квантования составляет
ε =
С –
Сfloat. (3)
Что касается промежуточных вычислений, то в формате ФТ представление результата умножения вещественных чисел конечным числом разрядов носит стохастический характер и, естественно, также требует процедуры квантования, результатом которой является стохастическая ошибка (шум квантования). Вопросам квантования вещественных данных посвящено много работ [1–4]. В целом можно отметить, что при высоком порядке фильтра (N > 10) весьма существенные трудности возникают уже при квантовании вещественных коэффициентов до 10–12 бит. Для аналитических подходов ошибки квантования считаются неустранимыми и приводят к искажению частотных характеристик цифрового фильтра, необходимости масштабирования его коэффициентов, появлению динамических шумов квантования, а также к возможности появления малых предельных циклов.
Однако ошибки аппроксимации и квантования могут быть устранены при проектировании цифрового БИХ-фильтра современными численными методами дискретного нелинейного программирования, позволяющими работать не с аналитическим, а с дискретным представлением характеристик фильтра (рис. 1б), когда как исходные требуемые, так и текущие характеристики табулированы с заданной дискретностью их представления в частотной области и в вычислительной системе представлены вещественными массивами. Это даёт возможность, с одной стороны, заменить процедуру аналитической аппроксимации простой оцифровкой требуемых частотных характеристик, причём ошибка оцифровки характеристик даже весьма сложной формы может быть минимизирована соответствующим выбором шага частотной дискретизации. С другой стороны, дискретное представление позволяет рассчитывать с заданной точностью все требуемые характеристики фильтра (включая и дисперсионные характеристики) применением численных методов. Каждая j-я характеристика фильтра, характеризуемая совокупностью (вектором) скалярных частотных выборок , позволяет применять для синтеза технического решения эффективные поисковые методы векторной оптимизации.
Неустранимую ошибку квантования коэффициентов также легко устранить полностью, осуществив дискретизацию и параметрического пространства коэффициентов фильтра перед его синтезом только теми значениями, при которых ошибка квантования (3) равна нулю. При этом математическое задание квантованного параметрического пространства возможно как вещественным (2), так и целочисленным кодом (1), что позволяет проектировать фильтры, использующие как вещественную, так и целочисленную арифметику вычислений и дискретизацию коэффициентов. Целочисленные цифровые фильтры (ЦЦФ) являются более универсальными и практически значимыми. Можно отметить следующие достоинства целочисленных цифровых фильтров.
1. Минимальная вычислительная сложность, так как в вычислительном алгоритме цифровой фильтрации любые операции над целочисленными операндами осуществляются значительно быстрее вещественных вычислений.
2. Целочисленные фильтры могут быть реализованы на любой цифровой платформе (MCU, DSP, FPGA) без наличия FPU (Floating Point Unit – сопроцессора) в структуре вычислителя.
3. Другим важным достоинством ЦЦФ является отсутствие процедуры квантования не только коэффициентов фильтра, но и результатов промежуточных вычислений, так как результат умножения целых чисел (например, текущего цифрового отсчёта и коэффициента фильтра) полностью детерминирован и не требует квантования для реализации на цифровой платформе с заданной разрядностью Wk представления данных. При заданной битовой разрядности квантования входного сигнала Wx достаточно выделить внутренний аккумуляторный регистр с разрядностью Wak = Wx + Wk бит для хранения результата целочисленного «умножения с накоплением» (МАС). Колебаний переполнения, то есть возникновения больших предельных циклов, вызванных переполнением разрядной сетки регистра-аккумулятора, при таком расчёте его разрядности практически никогда не возникает. Умножение с накоплением характерно при реализации как БИХ, так и КИХ цифровых фильтров. Данной операцией определяется и производительность цифровой системы. При этом для реализации целочисленных вычислений разработано большое разнообразие умножителей как последовательного, так и параллельного типа.
4. При целочисленном описании цифровые фильтры наиболее просто реализовать без умножителей, так как из натурального параметрического множества In легко выделить целочисленные подмножества коэффициентов , которые определяют замену умножителей сдвиговыми регистрами с заданным числом s сдвиговых сумматоров [5, 6].
5. Целочисленное решение легко преобразовать в вещественное квантованное решение формата ФТ, используя для этого их однозначную связь через соотношение (3).
Таким образом, при проектировании цифрового фильтра численными методами дискретного программирования осуществляется дискретизация как характеристик, так и параметров (коэффициентов) фильтра, что позволяет устранить как ошибки аппроксимации, так и ошибки квантования при практической реализации фильтра.
В данной статье рассматриваются вопросы дискретного моделирования рекурсивных каскадных фильтров, а также постановка и решение задачи синтеза по селективному и фазовому критериям в целочисленном пространстве коэффициентов как минимально-фазовых, так и линейно-фазовых БИХ-фильтров.
Целочисленная модель каскадного БИХ-фильтра
В настоящее время построение как БИХ-, так и КИХ-фильтров в форме каскадного соединения звеньев второго порядка на практике используется наиболее часто. Передаточная функция для рекурсивного ЦЦФ, состоящего из каскадного соединения m-звеньев второго порядка (
m =
N/2, где
N – общий порядок фильтра), имеет следующий вид:
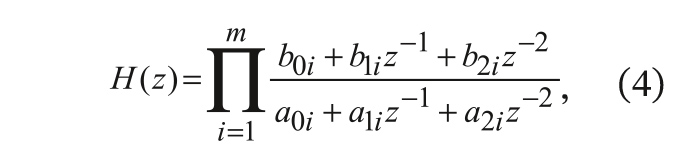
где комплексная переменная
z при переходе к описанию частотной характеристики
K(ejwT) = |K(ejwt)|•
ejφ(ωT) принимает значение
z =
ejωT, где
Т – период дискретизации.
Все коэффициенты передаточной функции (4) квантованы целочисленным её квантом (1), а их интервал изменения определяется заданной длиной битового слова (разрядностью) коэффициентов фильтра. Из соотношения (4) легко получается разностное уравнение для одного звена целочисленного фильтра:
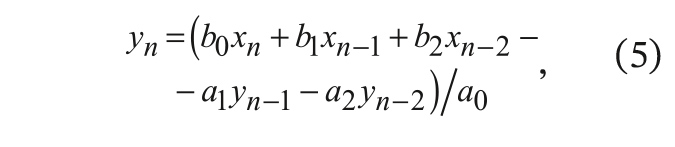
где
xn,
yn – целочисленные входная и выходная временны́е последовательности,
а0 – нормирующий коэффициент pоwer-оf-twо:
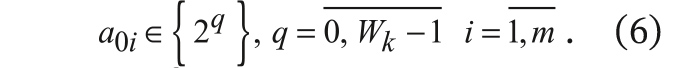
.
На рис. 2а приведена типичная структура звеньев рекурсивного целочисленного фильтра, соответствующая разностному уравнению (5). Как видно, при вычислении отклика фильтра кроме традиционных операций сложения, умножения и задержки на такт присутствует операция сдвига на B = log
2a
0 бит, с помощью которой реализуется целочисленное деление на нормирующий pоwer-оf-twо коэффициент.
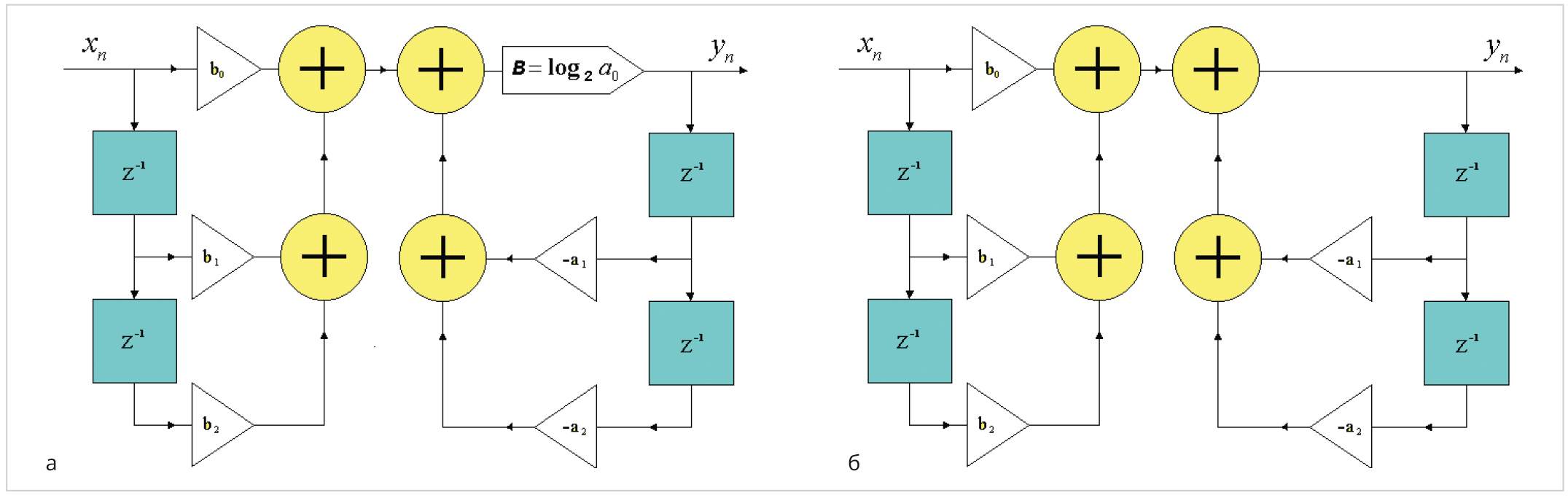
Для рекурсивного вещественного квантованного фильтра в каскадной форме построения передаточная функция имеет следующий вид:
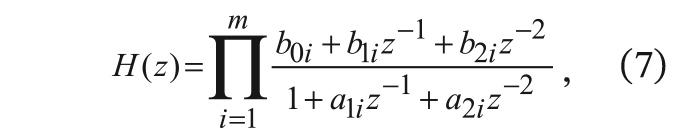
,
а разностное уравнение звена выглядит так:
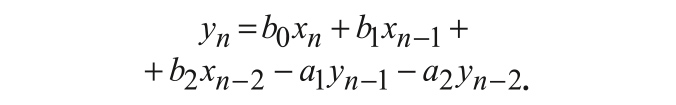
Здесь все значения коэффициентов задаются на единичном интервале их изменения вещественным квантованным значением (2). Структура звеньев прямой формы рекурсивного каскадного фильтра представлена на рис. 2б.
Условие устойчивости проектируемого БИХ-фильтра можно представить так:
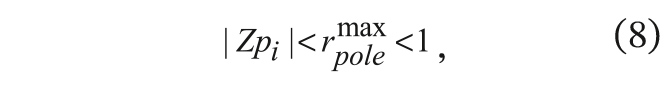
где
rpolemax – допустимый максимальный радиус полюсов передаточной функции фильтра в z-плоскости, при котором предельные циклы в рекурсивной системе не возникают.
Малые предельные циклы возникают, как известно, когда при отсутствии сигнала на входе амплитуда выходного сигнала затухает, но из-за вычислительных погрешностей не доходит до нуля, принимая зачастую колебательный характер. Возможность их возникновения возрастает с увеличением порядка рекурсивного фильтра и во многом определяется добротностью полюсов его передаточной функции (4), (7). В настоящее время провести теоретический анализ, расчёт предельных циклов непросто даже для БИХ-фильтров малого порядка. Поэтому действенной, а порой и единственной альтернативой является практическая реализация синтезированного фильтра на конкретной цифровой платформе (MCU, DSP или FPGA) и экспериментальный анализ амплитуды выходного сигнала при нулевом входе. В том же случае, когда предельный цикл наблюдается, действенной мерой его устранения является проведение повторного синтеза фильтра под меньшую допустимую добротность его полюсов.
А так как добротность полюсов пропорциональна их радиусу в z-плоскости, то достаточно задать меньшее значение допустимого радиуса полюсов передаточной функции в интервале условия (8) и вновь синтезировать фильтр.
При синтезе минимально-фазовых БИХ-фильтров аналогичное условие, как уже сказано, должно выполняться и для нулей коэффициента передачи
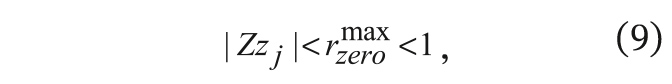
где
rzeromax – допустимый максимальный радиус нулей в z-плоскости.
Синтез методами дискретного нелинейного программирования позволяет реализовать любое значение максимальных радиусов как полюсов, так и нулей коэффициента передачи при решении конкретной проектной задачи [7, 8]. Как показала практика, при синтезе с меньшим значением максимального радиуса полюсов практически всегда удаётся получить проектное решение без предельных циклов того или иного рода, хотя селективная способность рекурсивного фильтра при этом, естественно, снижается. Синтез со значением максимального радиуса нулей в интервале (9) позволяет получать различные варианты минимально-фазовых фильтров.
Как известно, в каскадных формах построения цифровых фильтров необходима процедура масштабирования сигнала, то есть равномерной раскладки усиления по каскадам. Это позволяет фильтру работать в широком динамическом диапазоне входных сигналов. Однако расчёт такого масштабирования ЦЦФ гораздо легче осуществлять не стандартным применением Lр-нормы, а прямым введением требования обеспечения малого разброса коэффициентов передачи отдельных звеньев при дискретном синтезе фильтра [7]. Как показывает практика, существенного сужения динамического диапазона не происходит, если максимальные коэффициенты передачи его каскадов различаются не более чем в 3–5 раз. При более грубом покаскадном масштабировании сужение динамического диапазона фильтра становится заметным. Формально требования масштабирования сигнала записываются двусторонними функциональными ограничениями (15) экстремальной задачи дискретного синтеза.
Постановка задачи дискретного программирования
В общем виде задачу целочисленного нелинейного программирования (ЦНП) при машинном синтезе каскадного БИХ-фильтра с заданной разрядностью Wk представления коэффициентов можно записать так:
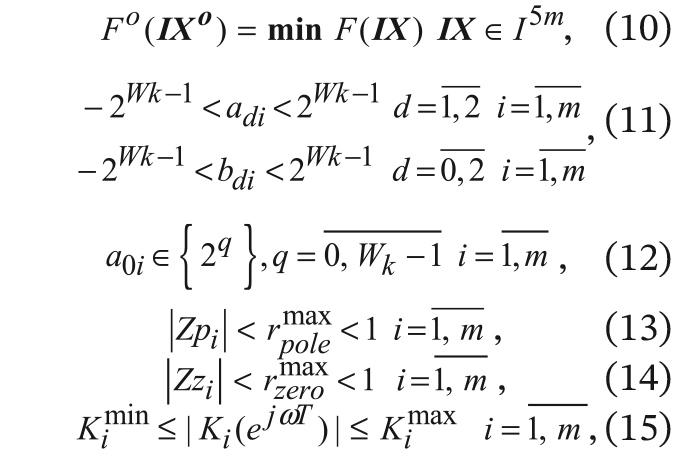
где
m – число звеньев (каскадов) второго порядка,
d – индекс коэффициента передаточной функции звена (4),
IX – вектор многомерного пространства квантованных целочисленных коэффициентов,
F(
IX) – целевая функция,
Kimin ,
Kimax – допустимые границы изменения коэффициента передачи
i-го звена фильтра.
Как видно, экстремальная задача синтеза (10) записана относительно целочисленного пространства
I5m параметров (квантованных коэффициентов фильтра) размерностью 5
m. Прямые ограничения (11) задают границы их изменения, функциональные ограничения (13) контролируют в процессе синтеза условие устойчивости рекурсивного фильтра по всем полюсам коэффициента передачи с радиусами, не превышающими
rpolemax,
а ограничения (14) контролируют в процессе синтеза нули коэффициента передачи при синтезе минимально-фазовых вариантов БИХ-фильтров. Ограничения (15) масштабируют коэффициенты передачи звеньев в заданный интервал. В алгоритме минимизации реализация функциональных ограничений осуществляется применением штрафных функций [9, 10].
Численное решение экстремальной задачи (10) в квантованном пространстве коэффициентов формата ФТ возможно только применением сеточных алгоритмов поисковой минимизации, когда дискретность сетки поиска задаётся числом двоичных разрядов
Wk, которыми в кодовом пространстве отображается каждая i-я переменная. Этим требованиям вполне отвечает поисковый алгоритм глобальной минимизации полимодальных целевых функций на детерминированной сетке [7, 10]. Построение минимизирующей последовательности на дискретной сетке формата ФТ в данном алгоритме осуществляется при помощи так называемых сфер поиска с изменяющимися радиусами. Таким образом, при последовательном автоматическом расширении и сужении сфер поиска происходит направленное сканирование всей дискретной области поиска без полного её перебора. Характерными особенностями данного поискового алгоритма является высокая надёжность отделения глобального экстремума, малые потери на поиск, эффективная работа в пространстве высокой размерности, а также отсутствие априори настраиваемых параметров.
Многофункциональное задание целевой функции в проектных задачах обычно формируется в виде взвешенной суммы частных целевых функций fi(IX), которые определяют выполнение функциональных требований по той или иной частотной характеристике фильтра:
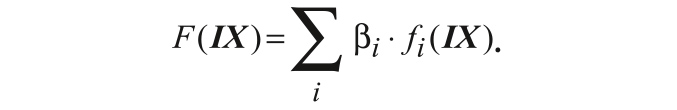
Коэффициент β
i задаёт значимость (вес) характеристики. Сами частные целевые функции
fi(
IX) наиболее часто формируют по критерию минимума среднеквадратичного отклонения
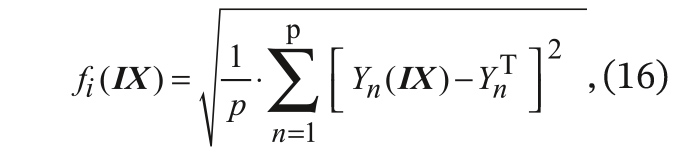
где
Yn(
IX) – текущее значение характеристики фильтра на n-й дискретной частоте диапазона определения, а
YnT – требуемое значение частотной характеристики фильтра.
В некоторых случаях для формирования частных целевых функций используется и критерий максимальной ошибки
fi(
IX) = max |
Yn(
IX) –
YnT|. (17)
Вектор
IX0, минимизирующий скалярную полимодальную целевую функцию
F(
IX) на допустимом дискретном множестве (11), является Парето-эффективным решением задачи ЦНП-синтеза целочисленного фильтра по совокупности противоречивых характеристик.
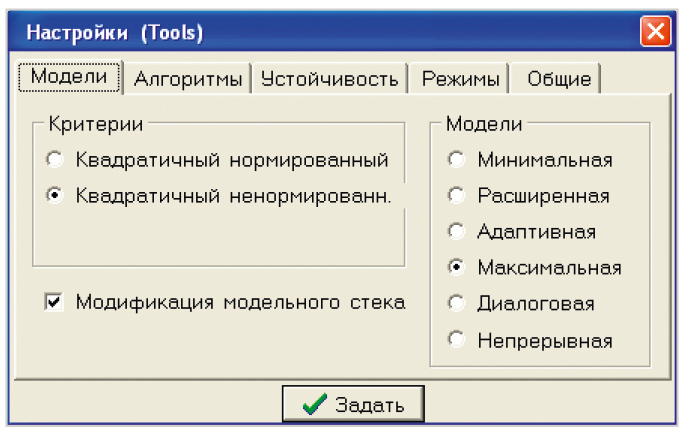
Следует отметить, что, в отличие от классического аналитического расчёта по аналоговому прототипу, поисковое проектирование является, безусловно, интеллектуальным процессом. Множество сценариев решения сложной проектной задачи может быть предложено, много специфических приёмов и навыков может быть применено опытным проектировщиком-поисковиком для успешного решения сложной задачи [7, 8]. Очевидно, что прямой сценарий решения сразу в многомерном пространстве параметров минимальной разрядности коэффициентов малоэффективен и не приведёт к приемлемому результату. Только в относительно простых задачах синтеза фильтров низкого порядка (N ≤ 10) удовлетворительное решение может быть получено подобным образом. Типовым же сценарием поискового синтеза каскадных фильтров высокого порядка является сценарий динамического программирования как последовательность поисковых задач с поэтапным повышением порядка проектируемого фильтра. На первом, стартовом этапе используют структуру низкого порядка (4-го или 6-го, не выше). Естественно, выполнение совокупных требований таким фильтром будет низкое. При этом для повышения надёжности отделения глобального экстремума в пакете ЦНП-синтеза на стартовом этапе желательно использовать максимальную или непрерывную модель поиска (рис. 3). На втором этапе уже данное решение используется в качестве исходного. Порядок фильтра при этом повышают добавлением ещё одного звена второго порядка, обычно путём дублирования найденных ранее коэффициентов одного из звеньев (что в пакете синтеза может делаться автоматически). После нескольких подобных итераций и определяется итоговый порядок проектируемого фильтра, при котором погрешность выполнения сложных совокупных требований лежит в пределах заданного допуска.
В качестве примеров рассмотрим дискретный синтез рекурсивных ЦЦФ по критериям селективных требований фильтра нижних частот (ФНЧ) в минимально-фазовом и линейно-фазовом вариантах проектируемого БИХ-фильтра.
Синтез рекурсивного минимально-фазового ФНЧ
Дискретный синтез 8-битового минимально-фазового ФНЧ десятого порядка в целочисленном пространстве квантованных параметров осуществлялся согласно следующим спецификациям.
- Полоса пропускания фильтра 0–1600 Гц
- Коэффициент передачи в полосе пропускания 0 дБ с допуском ± 0,25 дБ
- Переходная полоса 1600–2300 Гц
- Уровень подавления на частотах выше 2300 Гц не менее 30 дБ
- Фазовая нелинейность в полосе пропускания не выше 20°
- Длина слова коэффициентов Wk – 8 бит, включая знак
- Порядок рекурсивного фильтра: 10
- Максимально допустимый радиус полюсов: 0,95
- Максимально допустимый радиус нулей: 0,99
- Частота дискретизации 10 кГц
- Масштабирование коэффициентов передачи звеньев в интервал {0,9–5,0}
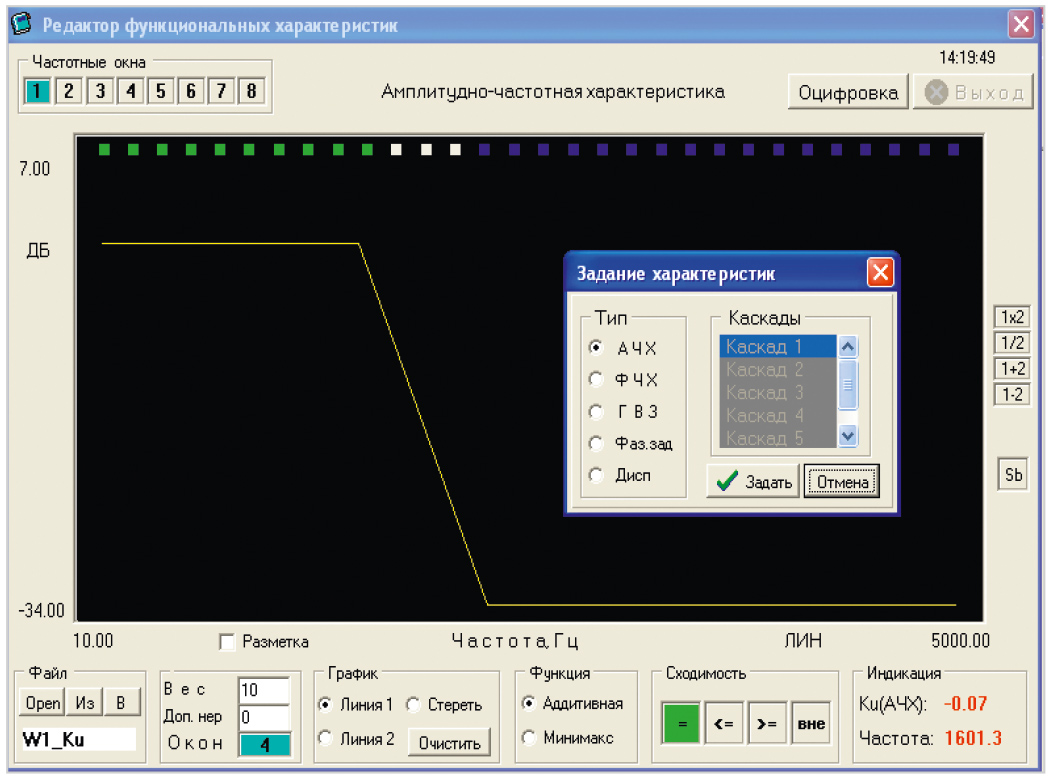
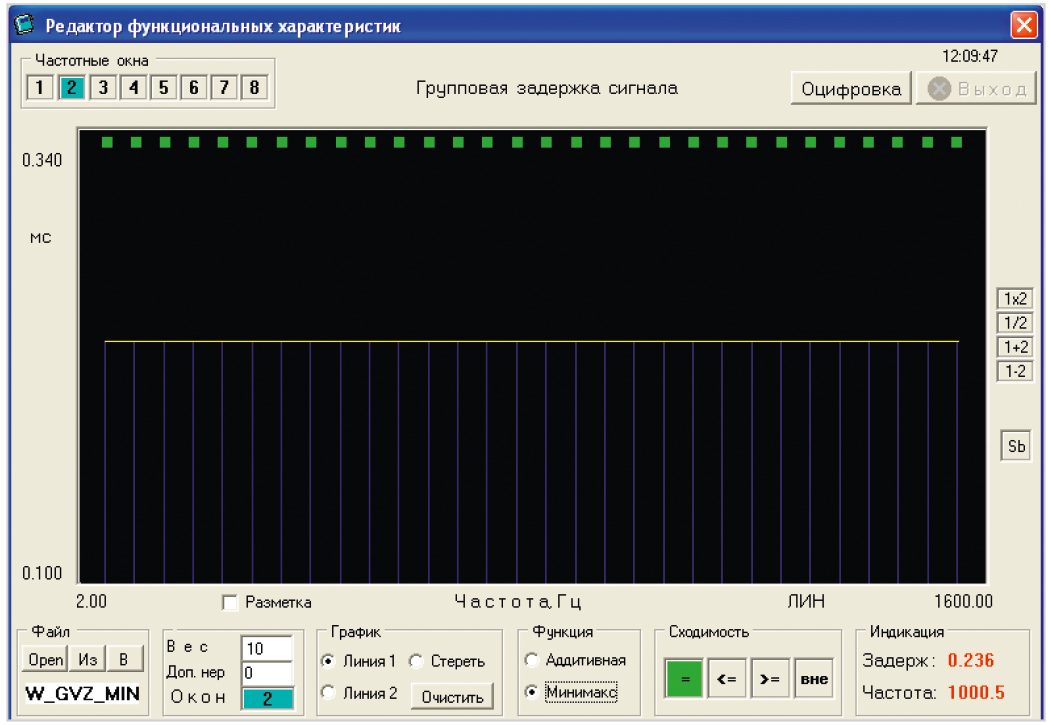
При синтезе БИХ-фильтра с требованиями фазовой линейности или, что то же самое, с постоянным временем группового запаздывания (ГВЗ) в полосе пропускания фильтра, целевая функция формировалась в виде взвешенной суммы двух частных целевых функций fАЧХ(IX) и fГВЗ(IX), обеспечивающих соответственно выполнение требований как к амплитудной селекции фильтра (рис. 4), так и к минимальной неравномерности его ГВЗ (рис. 5):
F(
IX) = β
1 fАЧХ (IX) + β
2 fГВЗ (
IX), (18)
где частная целевая функция
fГВЗ(
IX) определяется максимальным отклонением ГВЗ фильтра от требуемого значения τ
Т в полосе пропускания фильтра
fГВЗ(
IX) = Δτ
MAX = max | τ(
IX) –τ
T|, (19)
а целевая функция
fАЧХ(
IX) задавалась среднеквадратичной ошибкой (16) выполнения требований к АЧХ фильтра при одинаковой значимости требований к АЧХ и ГВЗ фильтра (β
1 = β
2).
Относительно целевой функции (18) задача целочисленного программирования для многофункционального синтеза минимально-фазового 8-битового ФНЧ в форме каскадного соединения 5 звеньев прямой формы второго порядка записывалась так:
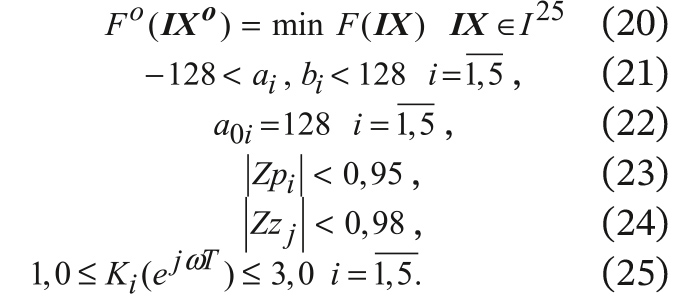
Таким образом, минимизация целевого функционала осуществлялась на 25-мерном целочисленном пространстве 8-битовых параметров в допустимой области (21) при выполнении функциональных ограничений устойчивости фильтра (23) по всем полюсам передаточной функции с радиусами, не превышающими 0,95 в z-плоскости, и всем нулям (24) с радиусами, не превышающими 0,98. Двусторонние ограничения (25) определяли масштабирование коэффициентов передачи звеньев фильтра в заданный интервал.
Для ввода структуры проектируемого фильтра в программу используем встроенный топологический редактор ЦНП-пакета [7], позволяющий сформировать файл исходных данных к решению конкретной задачи синтеза с указанием порядка фильтра, числа варьируемых коэффициентов, их начальных значений и границ изменения, а также возможного дублирования коэффициентов в случае необходимости.
В табл. 1 приведены оптимальные значения целочисленных 8-битовых коэффициентов передаточной функции минимально-фазового ЦЦФ, а графики его частотных характеристик представлены на рис. 6.
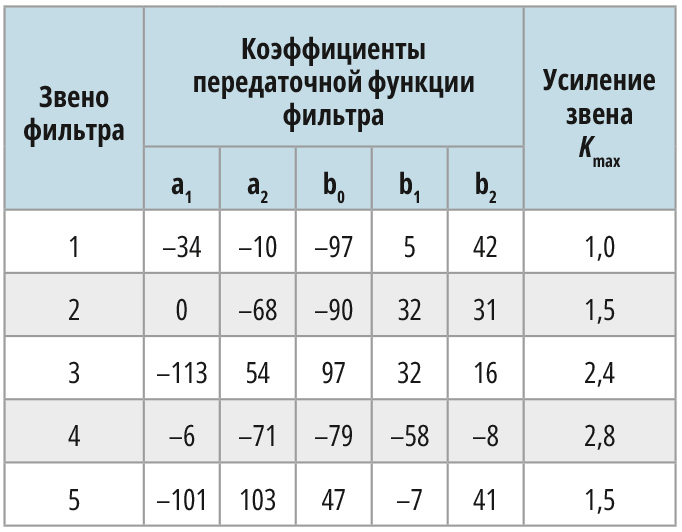
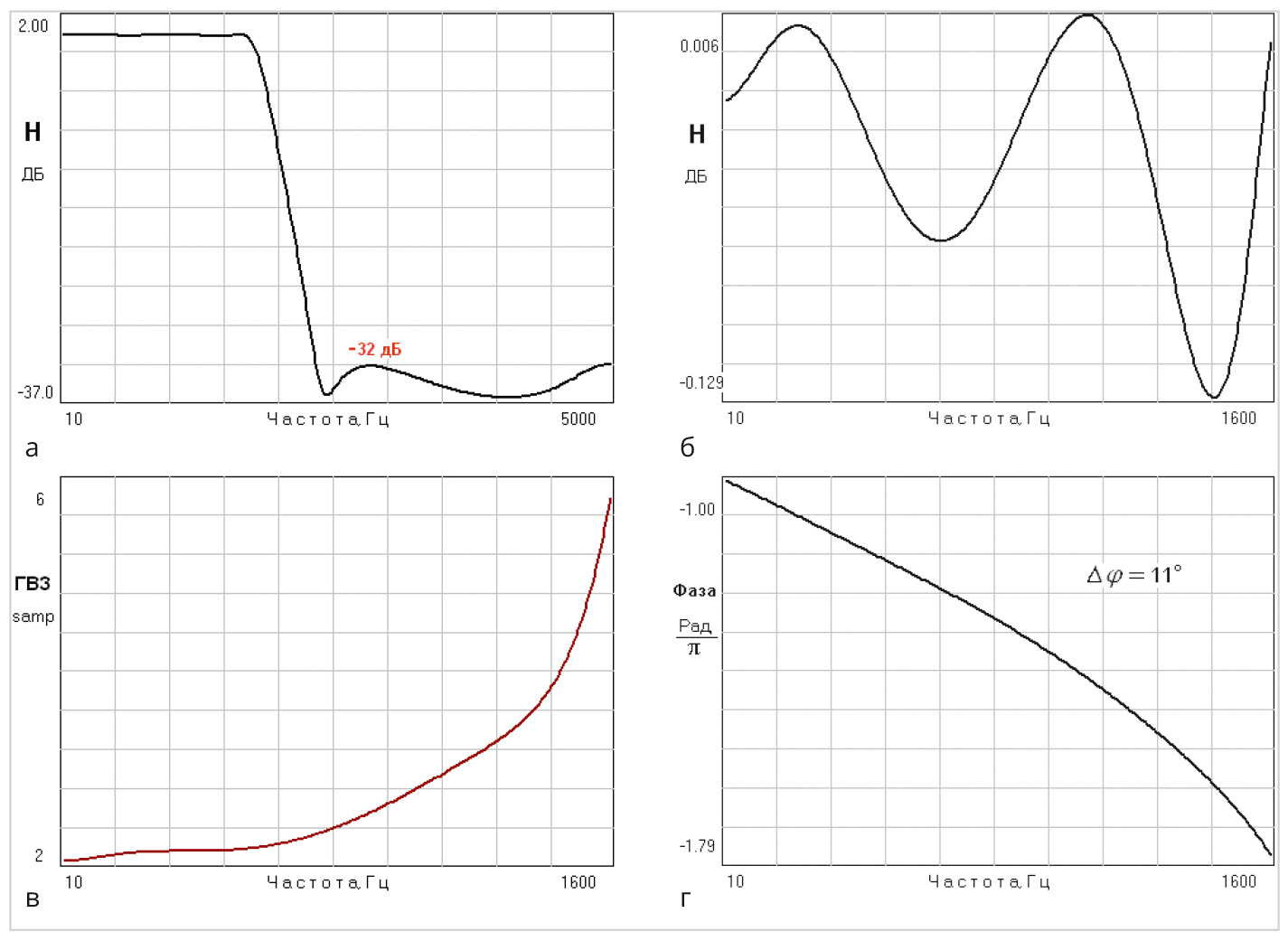
В данном случае неравномерность АЧХ в полосе пропускания 8-битового ФНЧ была равна ∆К = 0,23 дБ, а нелинейность ФЧХ составляла 11 градусов, что характерно для широкополосных минимально-фазовых как рекурсивных, так и нерекурсивных дискретных цифровых систем.
Исследуем профиль целевого функционала в точке целочисленного оптимума (табл. 1) путём построения его координатных разрезов. Графики разрезов подтверждают, что целевые функции в задачах многофункционального синтеза ЦЦФ имеют сложный, полимодальный характер. Дискретная минимизация таких функций является весьма непростой задачей. Тем не менее разработанный программно-алгоритмический поисковый комплекс пакета ЦНП-синтеза успешно справился с этой задачей, показав высокую надёжность и эффективность.
Практическая реализация фильтра осуществлялась на многофункциональном микроконтроллере MSP430 фирмы Texas Instruments с целочисленным RISC-ядром. Отличительными особенностями данного микроконтроллера является его низкое энергопотребление, невысокая стоимость, а также возможность только целочисленных вычислений. Измерение частотных характеристик фильтра осуществляется на реальном сигнале с помощью автоматизированной панорамной измерительной системы, разработанной в среде виртуальных приборов LabVIEW. Экспериментальные графики частотных характеристик фильтра на всём интервале Найквиста для частоты дискретизации fs = 2 кГц приведены на рис. 7.
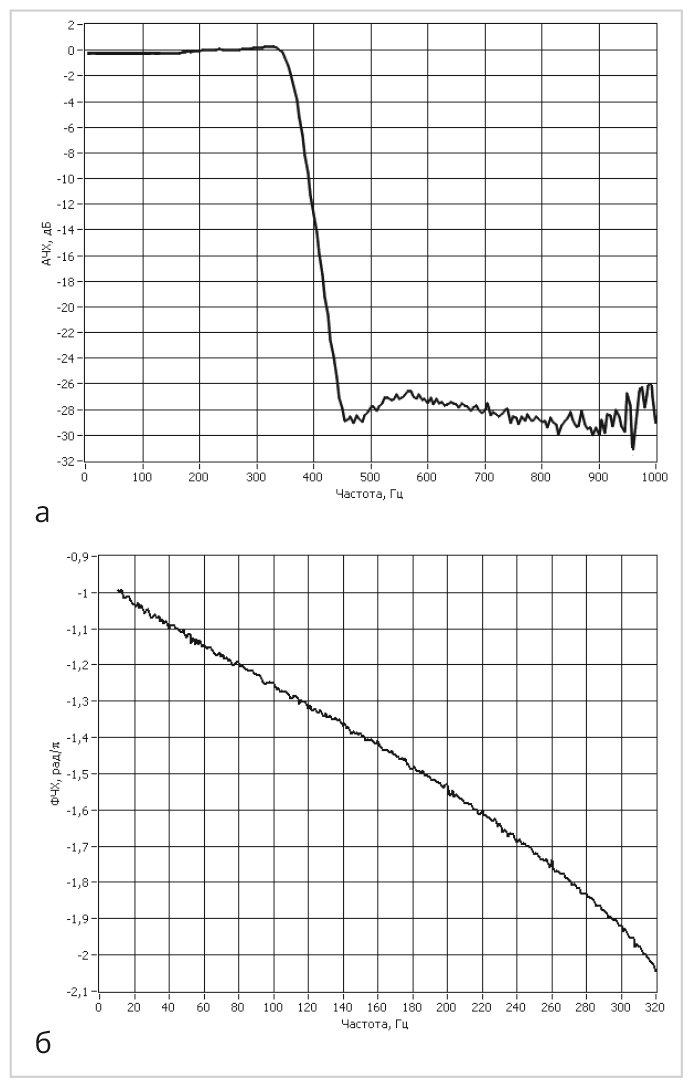
Анализ выходного сигнала при нулевом входе показал, что предельные циклы того или иного рода при максимальном радиусе полюсов 0,91 в синтезированном целочисленном ФНЧ отсутствуют.
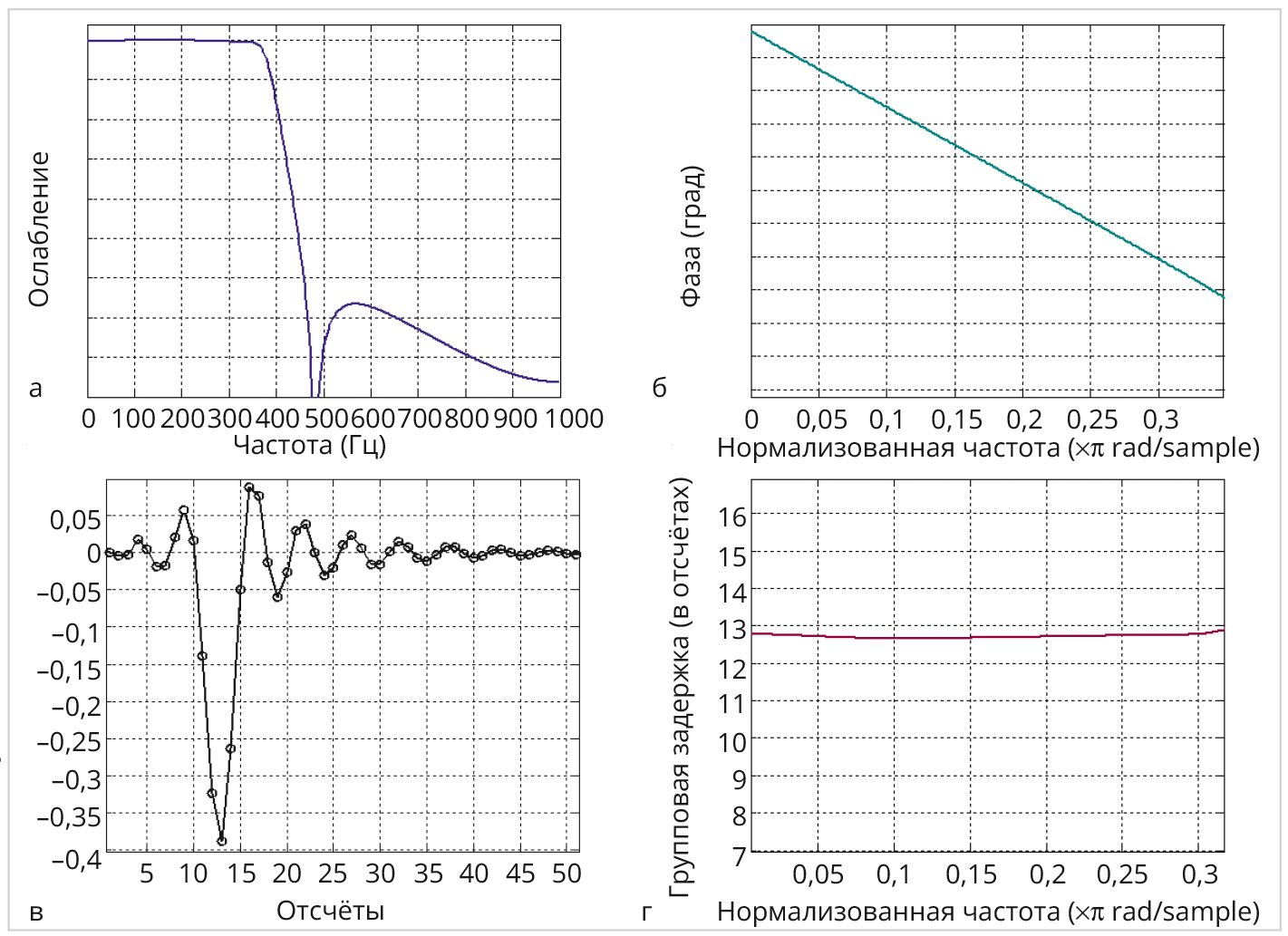
Вариант вещественных коэффициентов формата 8.7 по данной задаче приведён в табл. 2. Квантованные вещественные коэффициенты получены из целочисленных с помощью соотношения (2), определяющего их однозначное соответствие. Контрольный анализ характеристик по квантованным 8-битовым вещественным коэффициентам осуществлялся уже в пакете MATLAB. На рис. 8а – рис. 8в приведены частотные характеристики, а на рис. 8г – импульсная характеристика рекурсивного минимально-фазового БИХ-фильтра.
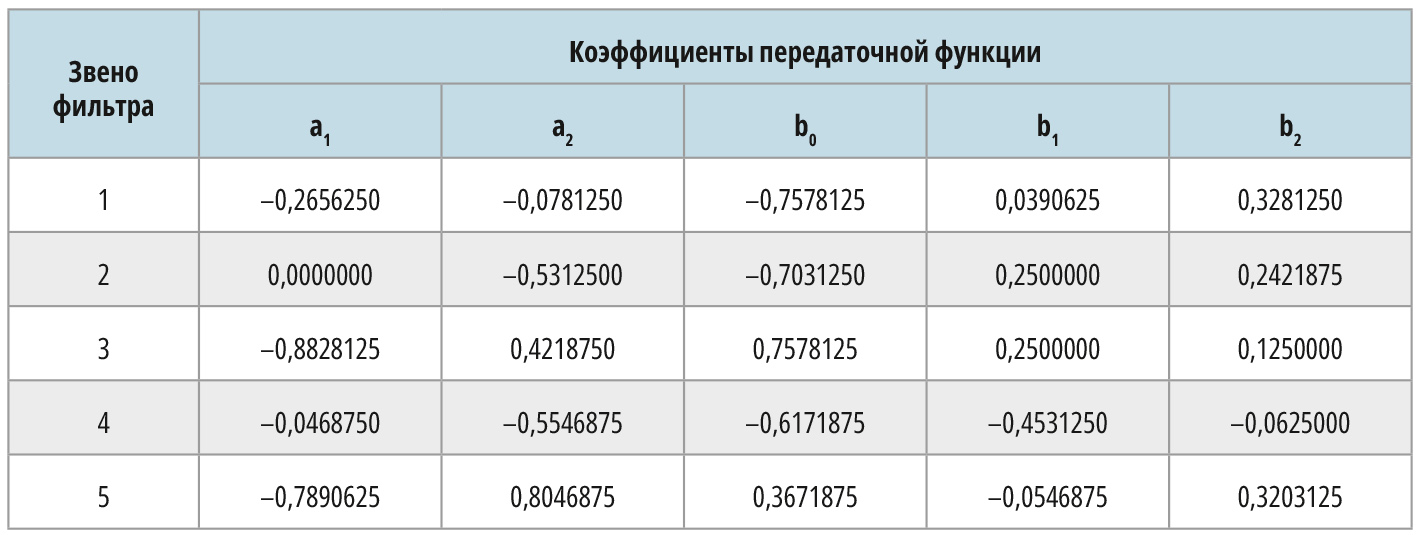
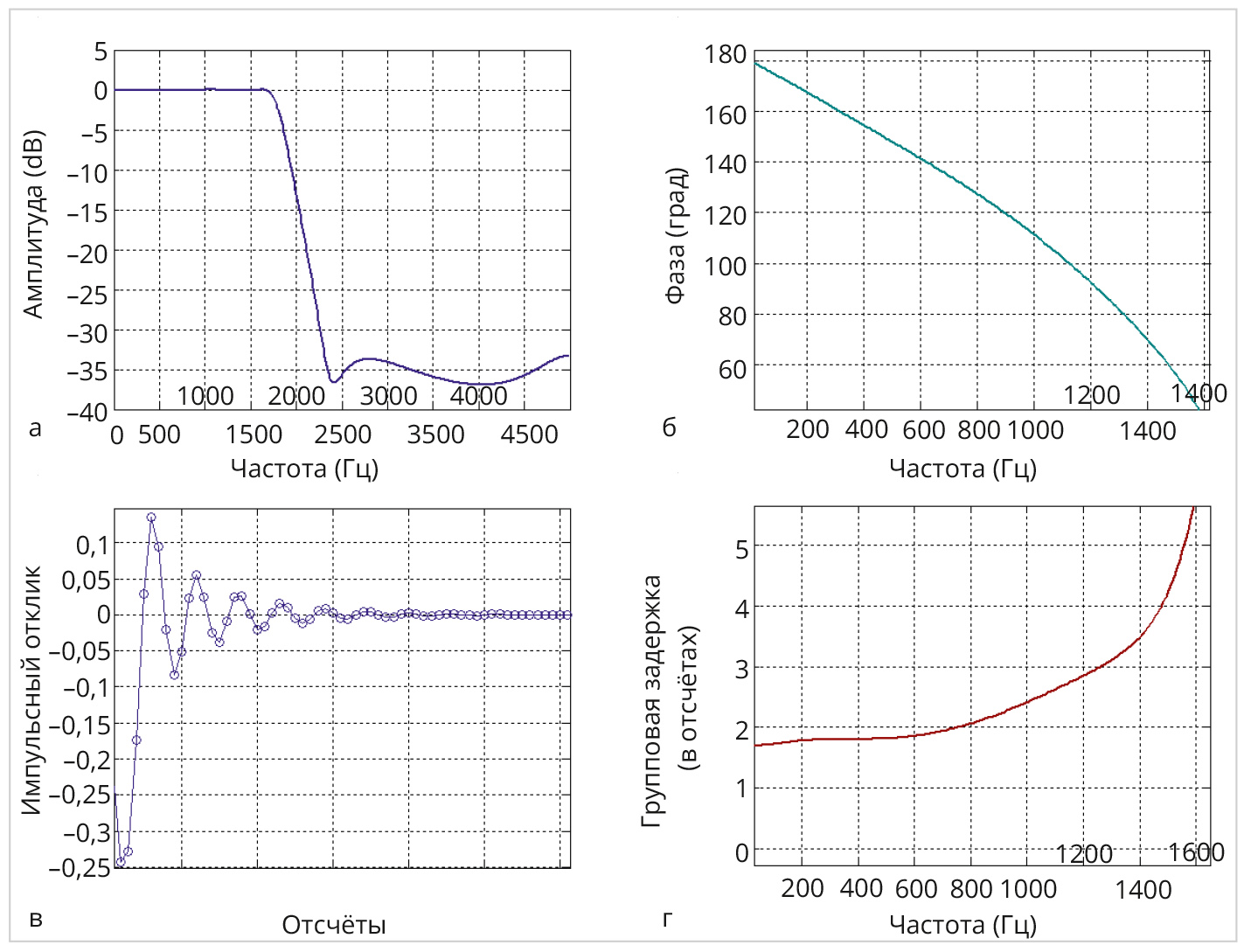
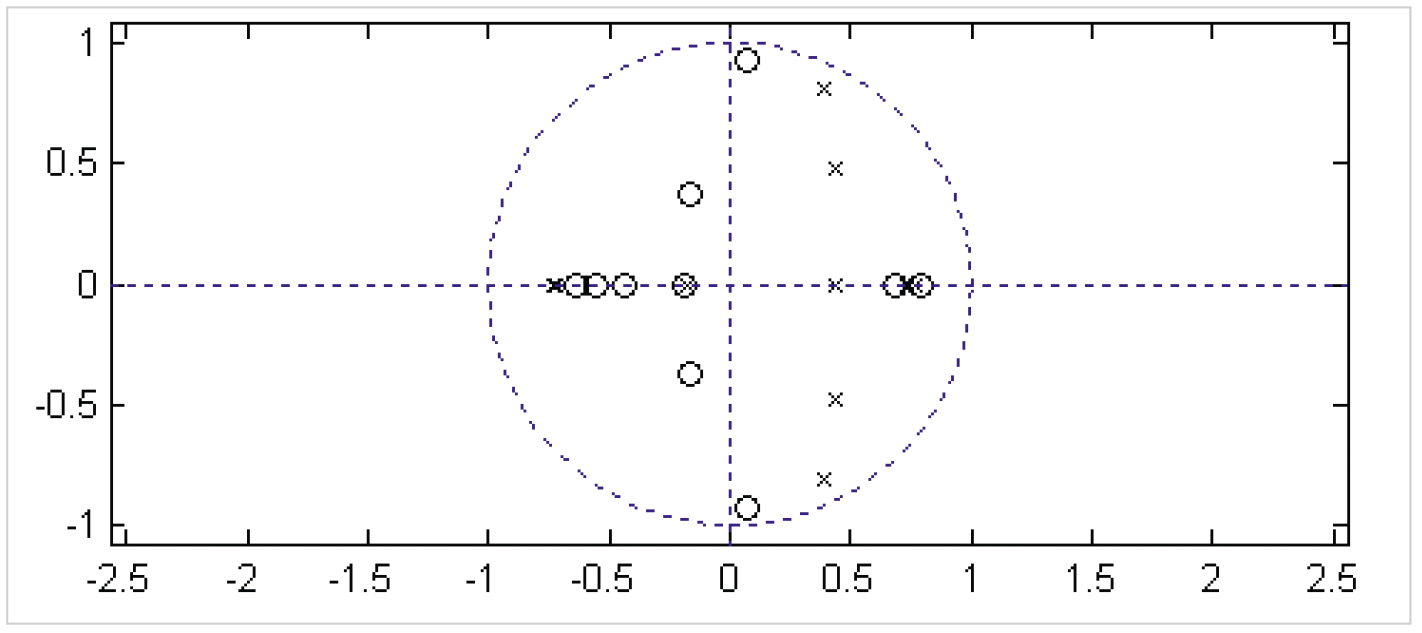
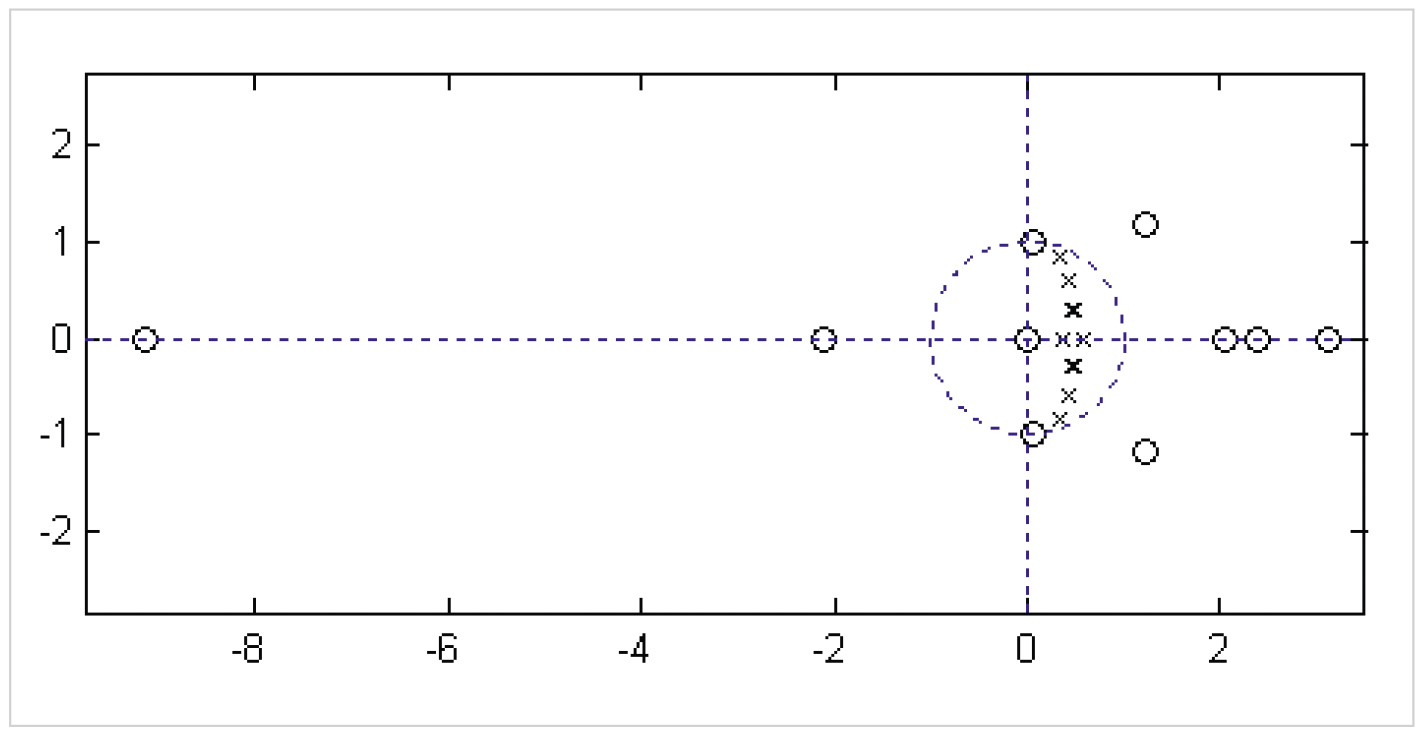
Как видно, анализ в пакете MATLAB полностью подтверждает синтезированные характеристики минимально-фазового БИХ-фильтра. На рис. 9 приведено распределение полюсов и нулей передаточной функции в z-плоскости. Видно, что полюса передаточной функции не выходят за границы (23) допустимого по синтезу максимального радиуса, а нули лежат внутри единичной окружности в z-плоскости. Это подтверждает, что синтезированный фильтр является минимально-фазовой дискретной системой. Таким образом, все функциональные требования при ЦНП-синтезе 8-разрядного ФНЧ десятого порядка были выполнены.
Любопытно сравнить решение, полученное ЦНП-синтезом, с классическим решением данной задачи билинейным преобразованием аналогового прототипа в пакете MATLAB, используя аппроксимацию требуемой АЧХ фильтра-прототипа по Чебышеву-2. На рис. 10 приведены характеристики по классическому синтезу рекурсивного ФНЧ десятого порядка с квантованием коэффициентов до 8 бит, а на рис. 11 – распределение его нулей и полюсов в z-плоскости для неквантованных коэффициентов.
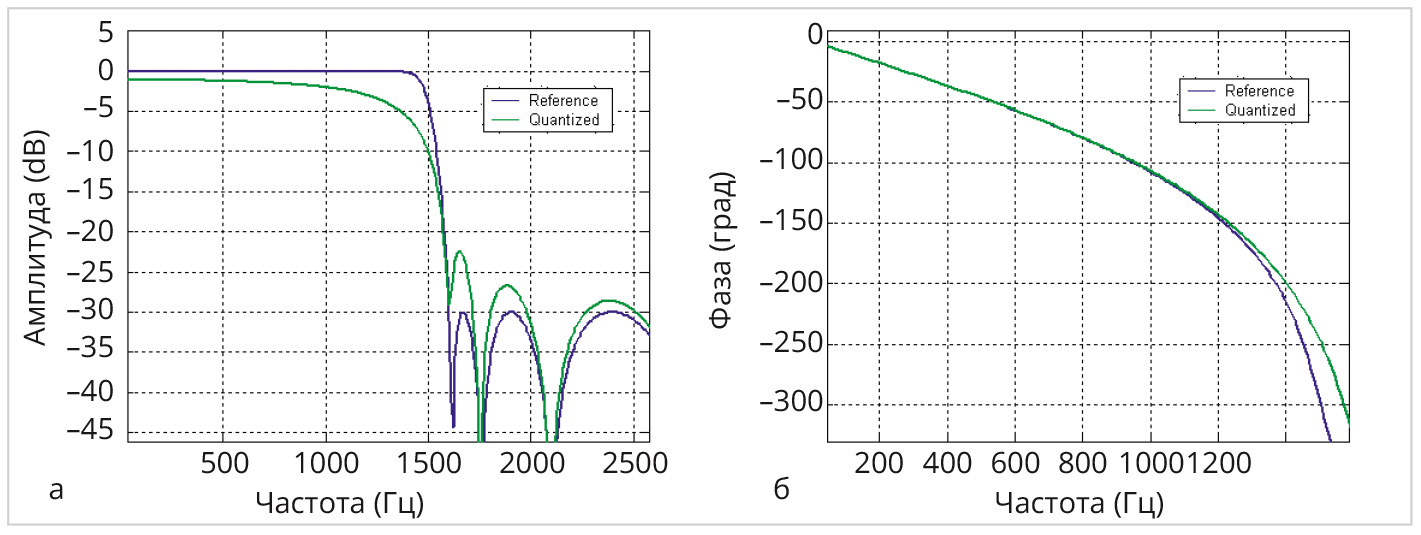
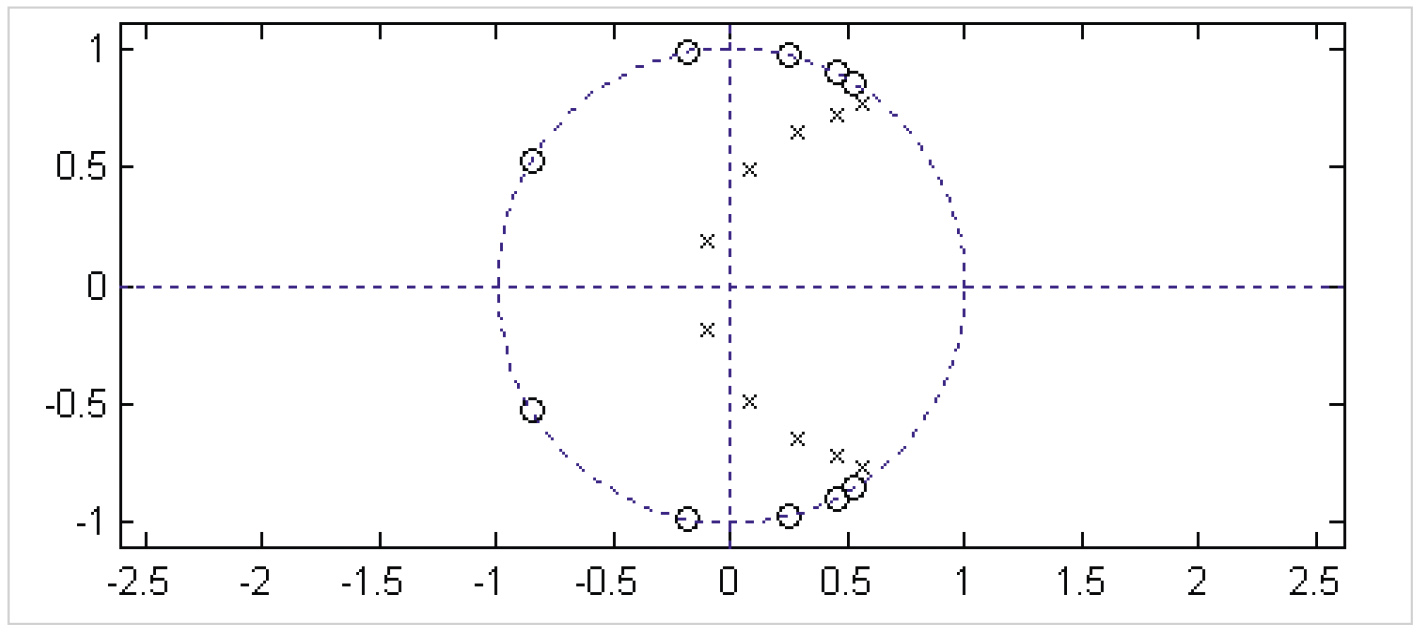
Видно, что при квантовании до 8 бит частотные характеристики рекурсивного ФНЧ 10-го порядка полностью не соответствуют спецификациям, а фазовая нелинейность превышает 70 градусов, что определяет чрезвычайно высокие дисперсионные искажения в полосе пропускания фильтра. Фазовые искажения очевидно меньше в варианте дискретного синтеза при распределении нулей как на, так и внутри единичной окружности в z-плоскости (рис. 8б, рис. 9). Однако лучшим вариантом обеспечения фазовой линейности в заданной полосе пропускания является вариант синтеза со свободным распределением нулей коэффициента передачи в z-плоскости, что вполне возможно реализовать методами дискретного нелинейного программирования. Покажем это на конкретном примере.
Синтез линейно-фазового рекурсивного ФНЧ
Синтез 8-битового линейно-фазового ФНЧ десятого порядка в целочисленном пространстве квантованных коэффициентов осуществлялся согласно приведённым выше спецификациям по синтезу минимально-фазового ФНЧ за исключением ограничений на распределение нулей коэффициента передачи БИХ-фильтра в z-плоскости. Целевые требования также определялись соотношениями (18) и (19) к амплитудной селекции и постоянству ГВЗ линейно-фазового фильтра в полосе пропускания.
Таким образом, относительно целевой функции (18) задача целочисленного программирования для многофункционального синтеза рекурсивного 8-битового ФНЧ в форме каскадного соединения 5 звеньев прямой формы второго порядка записывалась так:
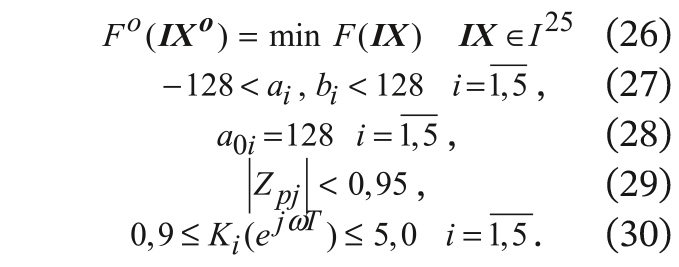
Время решения этой задачи на стандартном персональном компьютере не превышало 10 мин при использовании в качестве стартовой точки минимально-фазового решения. В табл. 3 приведены оптимальные значения целочисленных 8-битовых коэффициентов передаточной функции линейно-фазового ФНЧ, а в табл. 4 – их вещественный вариант.
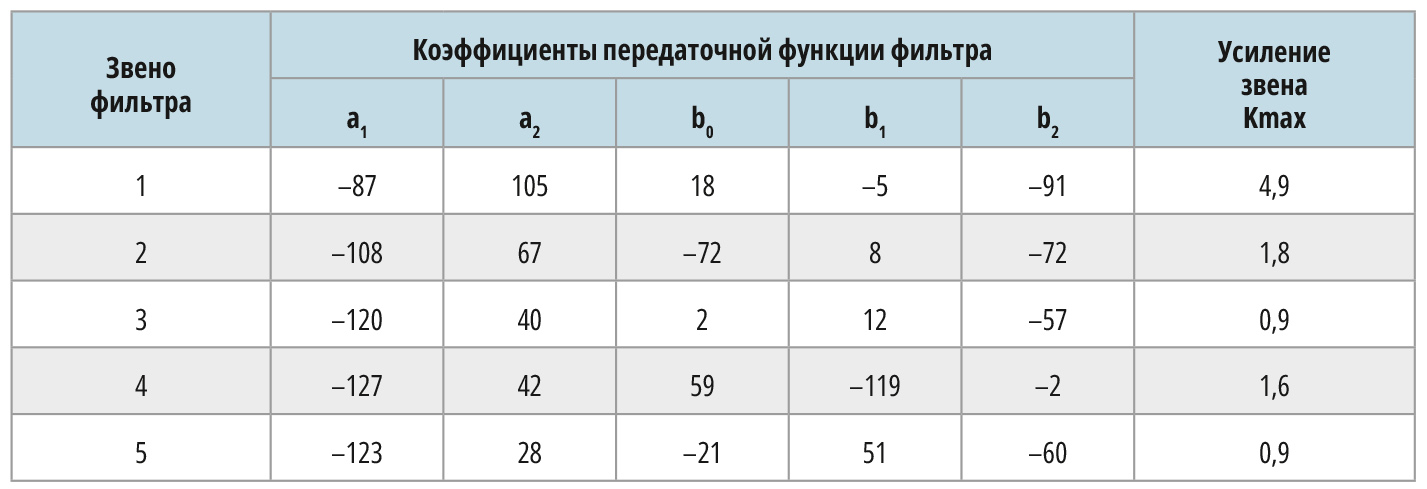
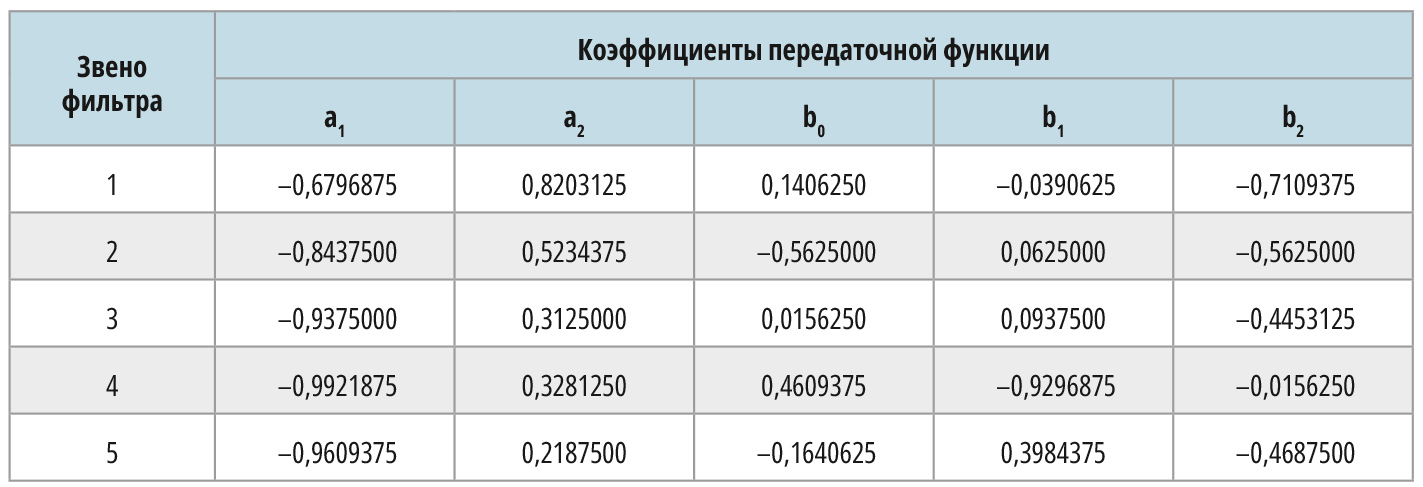
Оптимальные коэффициенты с помощью m-файла загружались в пакет MATLAB для анализа характеристик синтезированного каскадного 8-битового БИХ-фильтра во временно́й и частотной области (рис. 12). Как видно, требования амплитудной селекции при квантовании коэффициентов до 8 бит были полностью выполнены, причём неравномерность АЧХ в полосе пропускания ФНЧ не превышала 0,2 дБ при фазовой нелинейности менее одного градуса. Масштабирование каскадного фильтра осуществлено в заданном интервале, а Z-диаграмма (рис. 13) подтверждает свободное распределение нулей коэффициента передачи фильтра в z-плоскости, что и позволило обеспечить линейность его фазочастотной характеристики.
Практическая реализация фильтра в целочисленном варианте на МК MSP430F1611 полностью подтвердила синтезированные характеристики (рис. 14).
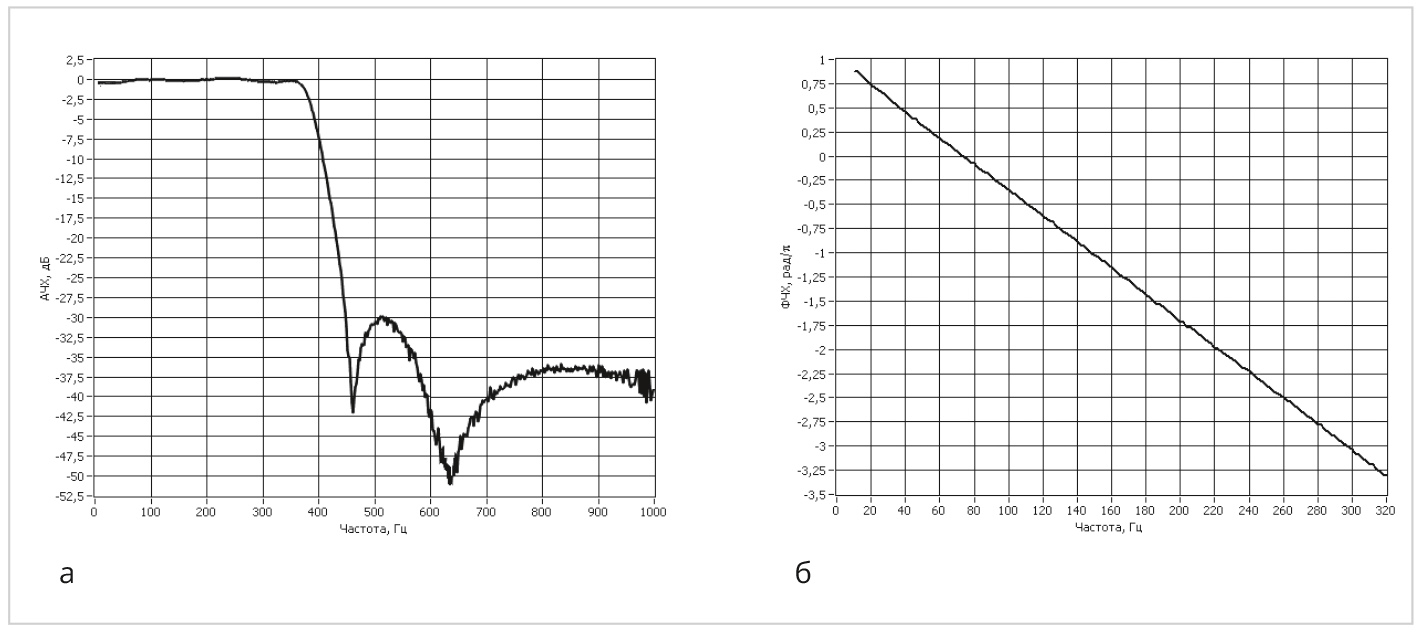
Анализ выходного сигнала при нулевом входе показал, что предельные циклы того или иного рода при максимальном радиусе полюсов 0,91 в синтезированном ЦЦФ также отсутствуют. Таким образом, все функциональные требования по синтезу 8-разрядного линейно-фазового ФНЧ были выполнены.
Сопоставляя результаты дискретного синтеза рекурсивного минимально-фазового и линейно-фазового ФНЧ, можно отметить, что при квантовании коэффициентов до 8 бит характеристики фильтров вполне соответствуют требуемым спецификациям, однако у минимально-фазового фильтра среднее время групповой задержки (4 семпла) существенно меньше, чем у линейно-фазового варианта (почти 13 семплов), что позволяет существенно уменьшить инерционность минимально-фазовой системы реального времени, сократить время расчёта отклика фильтра. Негативным же фактором является возрастание нелинейности фазочастотной характеристики минимально-фазового БИХ-фильтра вследствие существенного ограничения радиусов нулей его передаточной функции.
Обсуждение результатов
Методы дискретного нелинейного программирования в приложении к задачам проектирования линейных цифровых фильтров являются современной и перспективной альтернативой традиционным методам синтеза. Классическое проектирование базируется, как известно, на аналитическом представлении функциональных зависимостей, начиная с аналитической аппроксимации требуемой частотной характеристики фильтра, что, естественно, приводит к чрезвычайной сложности аналитических вычислений даже в относительно простых проектных задачах. Если же необходимо реализовать некий сложный закон изменения характеристики, например, фазы коэффициента передачи либо её производных (ГВЗ и частотной дисперсии), то аналитический расчёт фильтра становится невозможен. При этом можно отметить недопустимо низкое качество проектирования БИХ-фильтров в пакете MATLAB, никак не соответствующее современным требованиям. Ошибки аппроксимации фильтров-прототипов не позволяют проектировать рекурсивные фильтры со сложной, произвольной формой характеристик, а ошибки квантования на стадии реализации практически «рассыпают» частотные характеристики БИХ-фильтра, начиная уже с уровня 12-битового представления его коэффициентов даже при малом порядке фильтра, как это наглядно видно на приведённом в статье примере. Весьма негативным обстоятельством является и тот факт, что при любой аппроксимации в пакете MATLAB проектируются только минимально-фазовые версии БИХ-фильтров, причём в наихудшем их варианте с фиксацией всех нулей передаточной функции на единичной окружности в z-плоскости (рис. 11), что и определяет чрезвычайную нелинейность фазочастотной характеристики фильтра (рис. 10б). Фазовые искажения очевидно меньше в варианте дискретного синтеза при распределении нулей как на, так и внутри единичной окружности в z-плоскости (рис. 8б, рис. 9). Однако лучшим вариантом обеспечения фазовой линейности в заданной полосе пропускания является вариант синтеза со свободным распределением нулей коэффициента передачи в z-плоскости, что вполне возможно реализовать методами дискретного программирования. Таким образом, декларируемая нелинейность фазочастотных характеристик БИХ-фильтров никак не является их характерной особенностью, а определяется только несовершенством методик проектирования БИХ-фильтров через аналоговый прототип. Принципиальное отличие дискретного синтеза состоит в применении современных численных методов машинного проектирования, позволяющих работать не с аналитическим, а с дискретным представлением как характеристик проектируемого фильтра, так и его коэффициентов, что позволяет устранить систематические ошибки аппроксимации и квантования параметров. Применение алгоритма поиска на дискретной сетке квантованных параметров позволяет получать решения с нулевой ошибкой реализации на цифровой платформе или кристалле с заданной длиной слова коэффициентов. Поисковые методы дискретного программирования позволяют проектировать как минимально-фазовые, так и линейно-фазовые версии БИХ-фильтров, что важно в случаях, когда приходится устранять дисперсионные искажения, связанные с фазовой нелинейностью (например, при обработке речи и передаче данных). Современные алгоритмические комплексы дискретной минимизации позволяют решать такие проектные задачи надёжно и эффективно при выполнении всех внешних требований и ограничений к работе цифрового фильтра, что даёт возможность существенно повысить качество проектируемых БИХ-фильтров и сократить время их разработки.
Из материалов, приведённых в статье, видно, что, в сравнении с классическими аналитическими подходами, дискретный синтез численными методами нелинейного программирования позволяет следующее.
- Осуществлять проектирование фильтра по совокупности требуемых его частотных характеристик при произвольной форме их задания и заданной частотной шкале (линейной, логарифмической и др.).
-
Гарантировать устойчивость рекурсивного решения приоритетным выполнением функциональных условий устойчивости в процессе дискретного синтеза фильтра. При этом возможно задание требуемого максимального радиуса полюсов передаточной функции, что позволяет эффективно управлять добротностью проектируемого фильтра в случае возникновения предельных циклов того или иного рода.
-
Проектировать как минимально-фазовые варианты фильтров с нулями передаточной функции на или внутри единичной окружности, так и фильтры со свободным расположением нулей в z-плоскости, что позволяет значительно снизить фазовые и дисперсионные искажения.
-
Проектировать БИХ-фильтры с заданной разрядностью представления данных (вплоть до минимальных 3 бит) непосредственно на квантованном пространстве параметров (коэффициентов) фильтра.
-
Глобальная модельная идеология поиска определяет высокую надёжность отыскания эффективного решения экстремальной задачи нелинейного программирования. Хорошего начального приближения (прототипа) здесь не требуется. Как правило, в проектных задачах со сложными селективными требованиями оптимальное решение определяется не из начальной точки, заданной пользователем, а из точки, сгенерированной самим поисковым алгоритмом дискретной минимизации.
-
Необходимое масштабирование сигнала в каскадных структурах может быть обеспечено непосредственно в ходе дискретного синтеза фильтра. Здесь нет необходимости использования косвенных приёмов масштабирования усиления применением, например, Lp-нормы.
-
Целочисленная дискретизация пространства параметров (коэффициентов) фильтра позволяет получать проектные решения в целых числах, что обеспечивает минимальные вычислительные затраты при работе ЦЦФ в реальном времени и снимает все ограничения по арифметике вычислений при их реализации на любых цифровых платформах (сигнальных процессорах, контроллерах, FPGA) с заданной разрядностью представления данных, а также на кристаллах заказных или полузаказных СБИС.
Литература
- Emmanuel Ifeachor, Barrie Jervis. Digital Signal Processing: A Practical Approach (2nd Edition). Harlow: Pearson Education, 2002.
-
Rabiner L.R., Gold B. Theory and Applications of Digital Signal Processing. Englewood Cliffs NJ: Prentice-Hall, 1975.
-
Antoniou A. Digital Filters Analysis and Design. New York: McGraw-Hill, 1979.
-
Мингазин А.Т. Синтез передаточных функций цифровых фильтров в области дискретных значений коэффициентов (обзор) // Электронная техника. Сер. 10. 1993. № 1, 2.
-
Бугров В.Н., Артемьев В.В. Синтез целочисленных рекурсивных фильтров без умножителей на неэквидистантном множестве параметров // Успехи современной радиоэлектроники. 2017. № 7.
-
Артемьев В.В. Проектирование рекурсивных цифровых целочисленных фильтров: дис. … канд. техн. наук. Н. Новгород: Нижегородский государственный технический университет им. Р.Е. Алексеева, 2018.
-
Бугров В.Н. Целочисленные цифровые фильтры: монография. Saarbrücken: Lambert Academic Publishing, 2017.
-
Бугров В.Н. Синтез целочисленных БИХ-фильтров минимальной длины слова коэффициентов // Цифровая обработка сигналов. 2017. № 2.
-
Zangwill W.I. Non-linear programming via penalty functions. Management Science. Jan 1967, Vol. 13 Issue 5.
-
Воинов Б.С., Бугров В.Н., Воинов Б.Б. Информационные технологии и системы: поиск оптимальных, оригинальных и рациональных решений. М.: Наука, 2007.

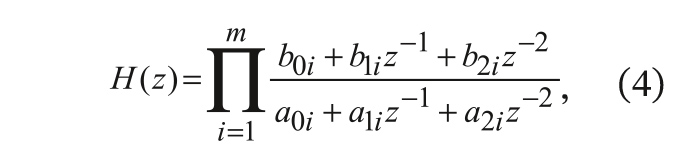
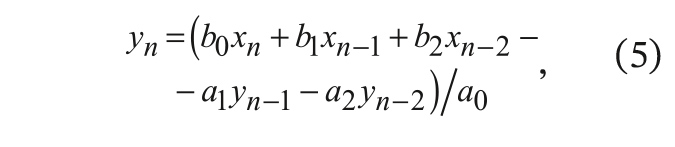
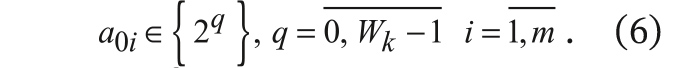 .
.
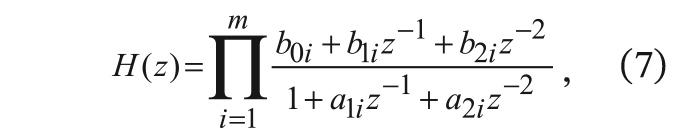 ,
,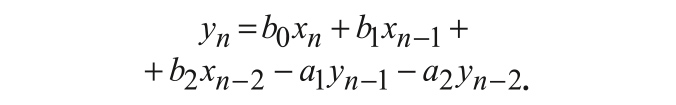
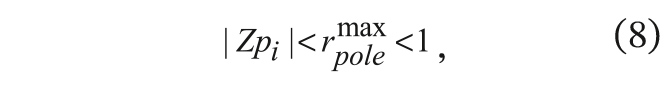
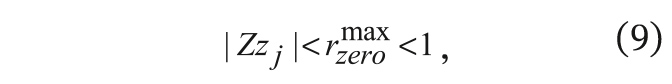
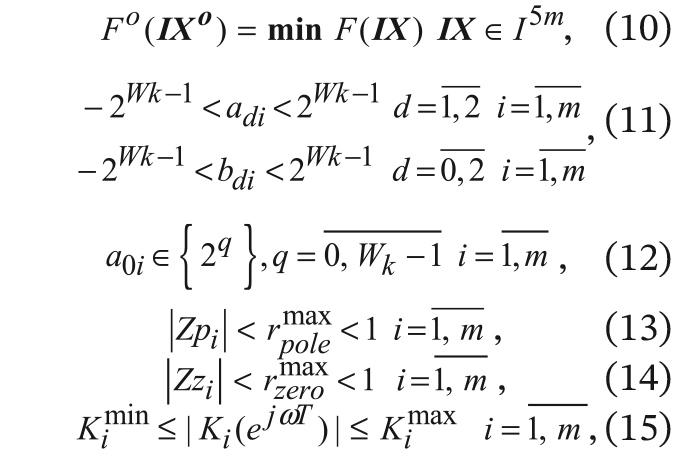
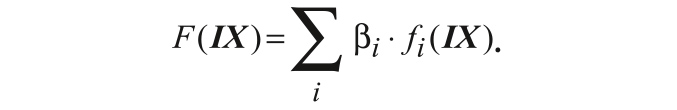
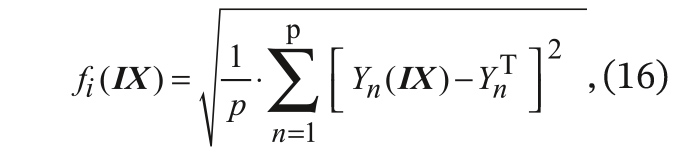



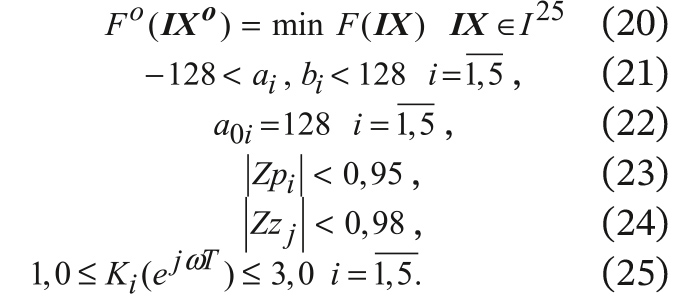








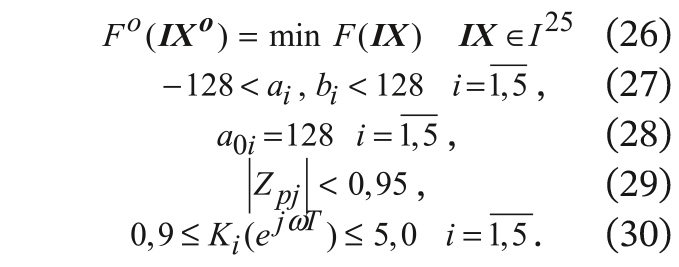





 электроника
электроника
 электроника
электроника
 электроника
электроника
 электроника
электроника